
Human Thistlethwaite Method
The Human Thistlethwaite Method is a method for solving a 3x3 Rubik's cube that is based on a computer algorithm. It's been adapted to be usable by humans by Ryan Heise in December 2002. The approach taken by the method is to reduce to cube to increasingly more restrictive sub groups of moves that are needed to solve the cube. This basically just means the cube isn't solved piece by piece but all the pieces are solved relative to each other until you arrive at the solved state.
Steps
Edge Orientation
The first step of this method is orienting the edges. If you already know how to do this, orient them and move onto the next step. If you don't, I'll go into detail below.
First things first, edge orientation refers to positioning your edges so that they can be solved using solely U, D, R, L moves. The front and back faces may only be turned 180° In speedcubing methods this is sometimes done to allow the cube to be solved without rotations of the whole cube cutting down on precious time. In our case, it simplifies the state of the cube so the algorithms are super simple later on.
To orient the edges you must first pick a top/bottom color pair and a pair for left/right. Those will be the faces you'll orient the edges with respect to. I should also mention that for this step and most of the others opposite colors of the cube will be regarded as the same due to symmetry. Now, edges have two possible orientations (as they have two sides) one of which satisfies the solvability condition we layed out earlier (the "good" edges) and the other which doesn't (the "bad" edges).

The first step of actually orienting the edges is to make out all the bad edges. This is done by looking at the colors of the highlighted tiles above and checking if a domninant color is on it. Here applies: U/D > L/R > F/B colors. So for example if you have white top and blue front, it's white/yellow > blue/green > red/orange, and for all edges the higher-ranking color of the piece needs to be facing the highlighted tile. Note that bad edges will always appear in pairs of two, so if you count an odd number of bad edges it's an indication you've miscounted!
Now that you've found all your bad edges, it's time to turn them into good ones. This is done by turning the front or back face 90° in either direction which will flip all four edges on that face, turning them from bad to good edges but also from good to bad. So all you need to do is manouver 4 of your bad edges onto the front or back face using only U, D, R, L moves and then flip them using F or B.
If you only have two bad edges or six which doesn't divide by four you'll need to put and odd number of bad edges on the front or back faces before flipping the edges. This way you can turn two or six bad edges into four. Then just solve those as explained above.
Double Cross
In this step we'll build a double cross on the top and bottom face where opposite colors are the same.
This is entirely intuitive and shouldn't be much of an issue. Just remember to keep the cube in the same orientation that you picked in step 1 and not turn the front or back faces. If you're stuck on how to insert the last edge, just move an already solved edge out of the way, move the empty slot back and then reverse the L/R move.
Orient Corners
This step isn't nearly as complicated as orienting the edges and everything can be done using one simple algorithm and its mirror variations. Below are the cases you can encounter with the corresponding algorithm solving two corners at once. If you're left with an odd number of bad corners, you won't encounter any of the cases listed. Instead, apply the algorithm to one pair of them which will solve one of the corners and orient the other so you can reach one of the positions below.




For clarity, the first move always pushes the front facing white piece onto the top or bottom layer.
Permute Corners
This step consists of two substeps after which all the corners will be permuted.
The first of these is to separate the white and yellow corners from each other so each side only shows one corner color. It doesn't matter if you put white or yellow on top and you can also ignore the colors of the edges. This is intuitive and doesn't involve any algorithms.
The second part is to match the side colors of the corners. There is a number of cases you can encounter which are listed below. Rotate the cube if your top and bottom faces are swapped but keep the left and right faces the same. In the graphs below the left square will show the top face and the right one will be the bottom layer.
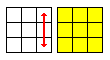
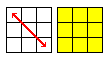
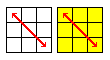

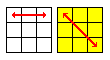
Permute Edges
In this step we'll position the edges in the top and bottom layer so that they're matching the corner pieces. As usual, opposite sides are treated the same, so a blue or green edge needs to be inbetween some combination of green and blue corners and an orange or red edge is to be put inbetween orange or red corners.
Wrongly permuted edges will only appear in pairs of two and the algorithm will swap four correctly permuted edges with four misplaced ones. If only two edges are left, just swap one of the bad edges with three good ones and you're left with four.
Also note that you don't have to worry about messing with the corners while setting up the edges for the algorithm. Just restrict yourself to double turns for the R, L, F and B faces to preserve what we need.

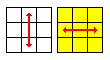
Double Turns
This is the last step of the solve and at this point the cube will be solvable using only double turns.
Of course you don't have to contrain yourself to that but I recommend solving the corners first using double turns and then fixing the edges as much as possible. This should be fairly intuitive and if you're stuck on the last four to six edges you can use whatever algorithms you know to complete them. The H perm is useful for two edge swaps and the U perm or knowledge of Roux is helpful for any three edge cicles.




♡2024 Please Copy.