
Belt Method
The Belt method is a broad category of methods where one starts by solving the four edges of the middle layer, the belt, before solving the rest of the cube. Many novice cubers have invented variations of this method independently and although quite easy to learn with a background in CFOP, they aren't competitively viable.
Steps
Belt
The first step is to solve the four edges of the middle layer which should only take a couple of moves.
Orient Outer Layers
In this step we'll orient the outer layers of the cube so that all white and yellow tiles are pointing up or down.
Setup
Start by getting an even number of top facing white and yellow edges onto one side. You can disturb the middle layer as long as all belt edges stay in the middle layer.
Then you need to make sure the OLL case you get is valid and solvable. This will depend entirely on the orientation of the corners since we already took care of the edges. To check if your position is valid, look at the corners and note that their white or yellow side is either facing the top, to the left or to the right. Now go through all four corners on one side and add up the directions of the white and yellow sides: top facing ones do nothing, pointing to the right adds one point and pointing to the left deducts one point. Your position will be valid precisely when the result is either 0, 3, or -3. You only need to do this for one side of the cube because if one side is in a valid position, the other will be too.
Once you've reached a valid OLL case you can solve it as normal for both layers.
Orienting Cross
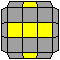

Orienting Corners
An x before the algortihm means you have to rotate the cube upwards so that the yellow side is facing the back before applying the algorithm.







Separate Colors
Now we'll be separating the white and yellow pieces from each other so we end up with one complete white side and a yellow one.
Start with the corners, which should be intuitive, then move on to the edges. While separating the corners, solve the belt if you disturbed it in the previous step. It's important you do this now because delaying it may result in encountering impossible PLL cases in the next and last step. If you know what you're doing you can still fix this later but it's better to just do it now while you still have more flexibility on the cube.
The edges can be solved using this simple algorithm.

Permute Outer Layers
After orienting the outer layers we'll permute them in this step to solve the cube.
If you have an invalid PLL case, perform M2 U2 M2 and the PLL cases on both sides will be possible.
An x' before the algorithm means you have to rotate the cube towards yourself so that the yellow side is facing you.
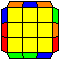
A perms
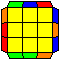
E perm
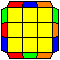
F perm
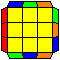
G perms
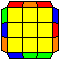
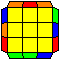
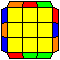
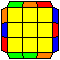
H perm

J perms
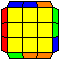
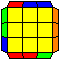
N perms
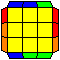

R perms
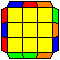
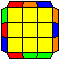
T perm
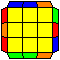
V perm

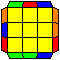
Y perm
♡2024 Please Copy.